

DAVIES, in Machine Vision (Third Edition), 2005 8.7 Concluding Remarksīinary images contain all the data needed to analyze the shapes, sizes, positions, and orientations of objects in two dimensions, and thereby to recognize them and even to inspect them for defects. For further information on grayscale morphological processing, see Haralick and Shapiro (1992) and Soille (2003).Į.R. For example, generalized dilation and erosion have acquired a central importance, since further vital concepts and constructs are based on them-closing, opening, template matching, and even connectedness properties (although space has prevented a detailed discussion of its application to the last two topics). In fact, mathematical morphology, as its name suggests, is mathematical in nature, and this can be a source of difficulty, 10 but there are a number of key theorems and results, which are worth remembering: a few of these have been considered here and placed in context. However, in the past few years, mathematical morphology has emerged as a unifying theory of shape analysis: we have aimed to give the flavor of the subject in this chapter. At first sight these may appear a somewhat random set, reflecting historical development rather than systematic analytic tools. As we shall see in Chapters 9 and 10 Chapter 9 Chapter 10, many simple small neighborhood operations exist for processing binary images and moving toward the goals stated earlier. The downside of having more pixels is that the file size will be bigger.Binary images contain all the data needed to analyze the shapes, sizes, positions, and orientations of objects in two dimensions, and thereby to recognize them and even to inspect them for defects. An image with a high resolution has more pixels, so it looks a lot better when you zoom in or stretch it. This results in images that look blocky or pixelated. In a low-resolution image, the pixels are larger so fewer are needed to fill the space.
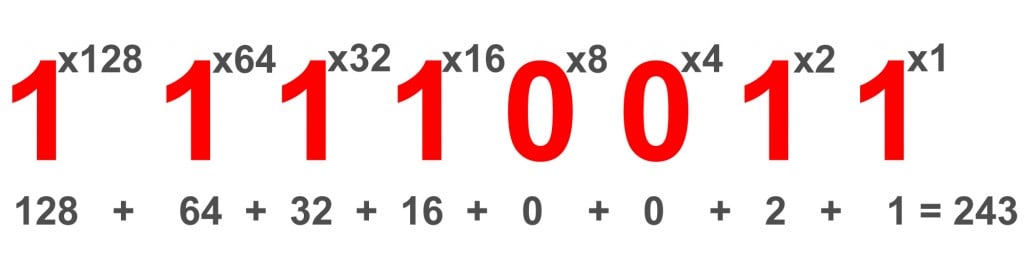
The resolution of an image is a way of describing how tightly packed the pixels are. Image quality is affected by the resolution of the image. This means that images that use lots of colours are stored in larger files. Images with more colours need more pixels to store each available colour. The number of bits used to store each pixel is called the colour depth.
While this is still not a very large range of colours, adding another binary digit will double the number of colours that are available: In binary this can be represented using two bits per pixel: Instead of using just 0 and 1, using four possible numbers will allow an image to use four colours. The system described so far is fine for black and white images, but most images need to use colours as well. This example shows an image created in this way: If the metadata for the image to be created is 10x10, this means the picture will be 10 pixels across and 10 pixels down. This data is called metadata and computers need metadata to know the size of an image. But before the grid can be created, the size of the grid needs be known. To create the picture, a grid can be set out and the squares coloured (1 – black and 0 – white). If we say that 1 is black (or on) and 0 is white (or off), then a simple black and white picture can be created using binary. Each pixel in an image is made up of binary numbers. Images also need to be converted into binary in order for a computer to process them so that they can be seen on our screen.


 0 kommentar(er)
0 kommentar(er)
